本帖最后由 xukun977 于 2020-4-11 13:47 编辑
[payamount]1.00[/payamount]
[pay]
下面略微详细一点解释这第三个问题。
例如对于无源LC滤波器,下图中的R1模拟的是电源内阻,这里设为25欧姆,
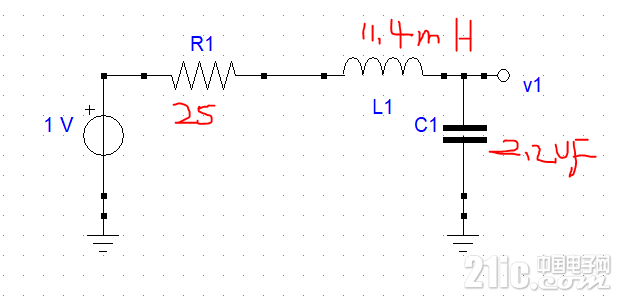
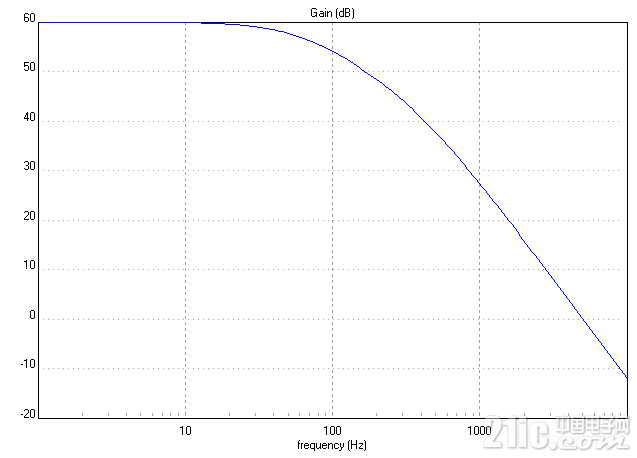
这个电路的传递函数和频率响应如下图:
1
--------------------------------------------
1+ ( C1 R1 ) s+ ( C1 L1 ) s^2

如上图所示,由于电感和电容的谐振作用,在频率为1000Hz频率点产生谢振峰,大约是10dB左右。
但是对于二阶RC电路,虽然和LC都是二阶的,但是无论如何调整电路参数,都不可能产生谐振效应,不可能有尖峰:

其频率响应曲线是单调下降的,没有尖峰的产生!
但是在上面的RC滤波基础之上,添加一个有源器件,可以是运放,可以是三极管,就可以得到与LC电路完全相同的频率响应。
上图中用流控电流源表示三极管,这个电路的频率响应,可以和上面的LC滤波器完全相同!!!!!!
具体工作原理:
对于LC滤波器,由于电感的电抗随着频率升高而升高,所以高频信号很难通过电感到达输出,而电容的电抗是随频率降低的,所以随着频率升高逐步短路信号到地。
一般性结论:
因为特征阻抗Z0=√(L/C)所以如果电容较大,电感较小,那么频率响应是欠阻尼响应;反之电容较小,电感较大,则特征阻抗大,Q值较小,此时是高阻尼响应。
√LC=1/w,w为谐振频率,所以上面L大,C小,或者是L小C大,我总可以保持LC乘积不变,也就是说谐振频率不变。
理解方法:
谐振频率不变,特征阻抗Zo变化,而电路Q=电阻R(这里是信号源阻抗,实际上也可以是负载阻抗)/特征阻抗,即Q=R/Z0
所以电感值较大,电容值较小,则Z0大,而Q与Z0成反比关系,所以Q较小,所以是高度阻尼。
或者这样理解,电阻R是谐振网络的负载电阻,当负载电阻相对于特征阻抗比较小时,R对LC谐振网络的影响就越重,此时频率响应下降较多在谐振频率附近。
而当电阻R和Z0两个电阻趋于平衡时,此时频率响应接近于临界阻尼状态,频率响应是平整的在谐振频率附近,没有尖峰或增益。
另一种极端情形是电感L比较小,电容值C大,则特征阻抗Z0相比于R较小,所以R对LC谐振网络的影响较轻,此时电路处于振荡边缘,而且在谐振频率附近,频率响应有个有个较大的电压增益或尖峰。
注:所谓的低Q近似,指的是Q<=0.5!
上面是无源LC低通滤波器的响应,下面看看是如果过渡到有源滤波器实现的。
不太严格的说,我们用有源器件取代电感。并先断开反馈环,并用三极管接成射极跟随器的组态:
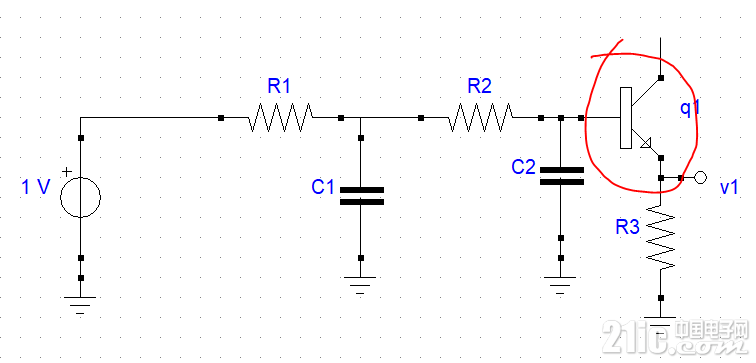
上图这个电路,是无源二阶滤波器,由于三极管基极输入阻抗特别高,所以电路相当于高阻尼响应。
也就是说,跟随器的作用是消除负载效应,利用其高输入阻抗、低输出阻抗的特性。
然后加入正反馈,路径是经C2引入:
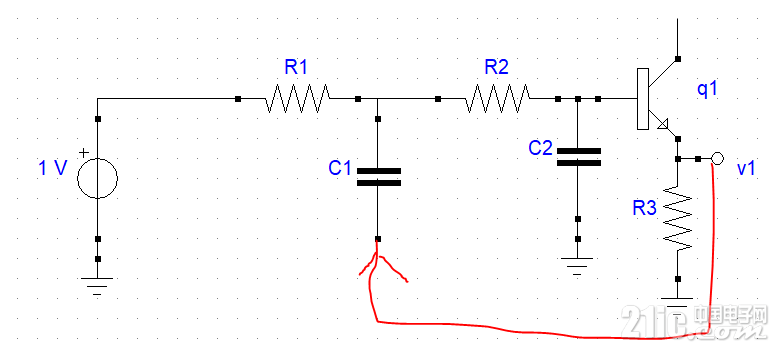
有源滤波的关键是:电容C1下端引脚不再接地了,而是连接到跟随器的输出,所以有个从跟随器输出到RC滤波器中点的正反馈!正反馈可以增强响应,减小阻尼,据此我们可以获得所期望的频率响应形状,这个方法和调整无源LC滤波器的中L和C之比一样的。
从能量的角度看,我们是通过有源器件从电源上获取能量,来弥补滤波器中电阻的损耗。正反馈连接只在谐振频率附近把过剩能量返回到滤波器,也就是说,这是个局部化反馈,这个特点是由反馈电容C1的电抗特性决定的:在低频时,电容电抗较高,于是在低频时这个正反馈没什么用。而在高频时,电容C2电抗较小,导致跟随器的输出电压幅度较小,此时尽管C1的电抗很小了,输出电压V1太低了,反馈回来的信号太弱了,可以忽略。
而在谐振频率附近,电容C2的电抗很高,电容C1的电抗很小,可以反馈回来较大的能量。
所以通过改变两个电容C1和C2的比值,可以改变阻尼程度,相当于调整无源LC滤波器中的L和C之比一样。而且与LC滤波器中的情形类似,这里的电阻和电容之积决定了滤波器的截止频率,只不过这里是两个电容和两个电阻完成的,而不是像LC滤波器,只需一个电感和一个电容来完成,也就是说,设计自由度大了。
从储能的观点看,两个电路都是有两个储能元件----一个是L和C,一个是C1和C2,所以两个电路都是二阶电路。
通过以上的措施和努力,我们可以让有源滤波器的频率响应和无源滤波器完全相同,目的也就实现了。
1,低频时,射极跟随器的输入阻抗,决定电路增益=1
2,高频时,电容C2的阻抗较小,V1较小,反馈回来的电压很小。
3,唯有中频RC2小,RC1大,且当V1越是1时,有增益增强,频率响应曲线上表现出尖峰。
所以C1/C2的比值很重要,可以调整Q值。
[/pay]
|