单位脉冲序列的m文件:
function [x,n] = impseq(n0,n1,n2)
if ((n0 < n1) | (n0 > n2) | (n1 > n2))
error('参数必须满足 n1 <= n0 <= n2')
end
n = [n1:n2];
x = [(n-n0) == 0];
调用例如:
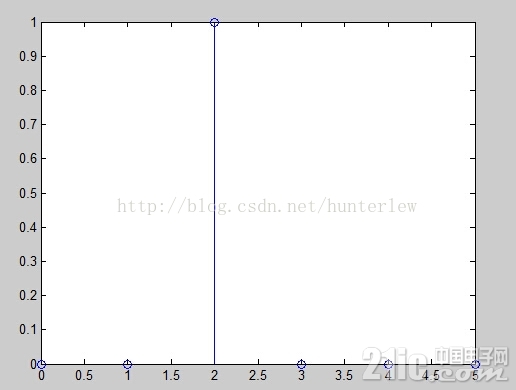
[x,n] = impseq(2,0,5); %表示从0开始共6个点,第二个点为1。
stem(n,x);
单位阶跃序列的m文件:
function [x,n] = stepseq(n0,n1,n2)
if ((n0 < n1) | (n0 > n2) | (n1 > n2))
error('参数必须满足 n1 <= n0 <= n2')
end
n = [n1:n2];
x = [(n-n0) >= 0];
调用:
[x,n] = stepseq(2,0,5);
stem(n,x);

另外我在测试的时候发现了这样的报错:Cannot find an exact (case-sensitive) match for...。这种情况好像是因为出现了大小写不同。
把文件名(包括.m)和函数名一律改为小写即可。
matlab中可以用y = conv(x,h)来计算两个有限长度序列的卷积。该函数无法得知位置信息,默认x和h位置向量都是从零开始。可以根据需要扩展。
这里注意,matlab默认序列从零开始,即为0:N-1。但是变量的下标(即括号中的序号)倒是从1开始的,即为1:N。
卷积的输出序列长度区间为n = 0:length(x)+length(y)-1。
说到卷积,则相关函数也是卷积的形式,例如x和y的互相关表示为y(m)和x(-m)的卷积,x的自相关表示为x(m)和x(-m)的卷积。
注意相关函数也是随n变化的。如果x和y的互相关在n0处有峰值,说明y和x移位n0后相似。
LTI系统可以用差分方程来描述。但差分方程不一定描述LTI系统,必须满足所谓的松弛条件。
matlab解差分方程可以用y = filter(b,a,x)来实现。b是x那边的系数向量,a是y那边的系数向量,x是输入序列。
此外,可以用[h,n] = impz(b,a,N)来求解h(n)。
|