|
百万京东E卡+大额优惠券!7周年钜惠震撼来袭→www。szlcsc.com/go/180531qzn;【20000元大奖】第三届立创电子制作节火热报名中→club.szlcsc.com/article/details_12591_1.html。
数学中有哪些看起来很不可思议的知识? 先来看个公式吧,这个尽管不难证明,但是还蛮有趣的~ 一.平面几何篇 1.(i)九点圆定理:三角形三边的中点,三条高的垂足,垂心与各顶点连线的中点这九点共圆。(九点圆又称欧拉圆、费尔巴哈圆) (ii)费尔巴哈定理:三角形的九点圆与其内切圆以及三个旁切圆相切。 (iii)库里奇-大上定理:九点圆的圆周上(任意取定)四点中任取三点做三角形,所有这四个三角形的九点圆圆心共圆。 2.西姆松(Simson)定理:过三角形外接圆上异于三角形顶点的任意一点作三边或其延长线上的垂线,则三垂足共线。(此线常称为西姆松线) 3.蝴蝶定理:设M为圆内弦PQ的中点,过M作弦AB和CD。设AD和BC各相交PQ于点X和Y,则M是XY的中点。(配个图啦啦啦~) 4.君知物理学中有家喻户晓的牛顿三大定律,殊不知平面几何中也有牛顿三大定理(别闹,当然是同一个牛顿),想当年刚知道时简直膜拜~ 牛顿定理1:完全四边形三条对角线中点共线。 牛顿定理2:圆外切四边形的两条对角线的中点,及该圆的圆心,三点共线。推广:和完全四边形四边相切的有心圆锥曲线的心的轨迹是一条直线,是完全四边形三条对角线中点所共的线。 牛顿定理3:圆的外切四边形的对角线的交点和以切点为顶点的四边形对角线交点重合。(四线共点) 5.帕斯卡(Pascal)定理:圆锥曲线内接六边形其三对边的交点共线,与布列安桑定理对偶,是帕普斯定理的推广。(至于后面两个是什么,戳进去看就好了,当年也只是知道是什么并没有用过~) 6.根心定理:三个两两不同心的圆,形成三条根轴,则要么三根轴两两平行,要么三根轴完全重合,否则三根轴两两相交,即此时三根轴必交于一点(三线共点),该点称为三圆的根心。(根轴是对两圆等幂的点集,是一条垂直于连心线的直线,特殊情形:若两圆相交,则根轴就是连接二公共点的直线;若两圆相切,则根轴就是过切点的公切线;) 7.五点共圆:(具体追根溯源请搜索密克(Miquel)定理)(不会证的孩纸还是先不要膜了,赶紧多读书,不然还是naive~~) 2000年12月20日,**主席出席澳门回归祖国一周年庆典活动期间,在参观濠江中学时向该校师生出了一道求证“五点共圆”的平面几何题:“假设:任意一个星形,五个三角形,外接圆交于五点。求证:这五点共圆。” 江主席出的这道平面几何题用规范的数学语言表述是这样的:在任意五角星AJEIDHCGBF中,△AFJ、△JEI、△IDH、△HCG和△GBF各自的外接圆顺次相交的交点分别为K、O、N、M、L。求证:K、O、N、M、L五点共圆。(确实很神奇~~) 8.**爪定理(我也想知道有没有好听一点的名字啊亲~):设△ABC的内心为I,∠A内的旁心为J,AI的延长线交三角形外接圆于K,则KI=KJ=KB=KC。(注意红线的形状) 9.拿破仑(Napoléon)定理(据说是行军打仗时证明的,也是厉害):向任何三角形三边分别向外侧作等边三角形,然后把这三个正三角形的中心连结起来所构成的三角形一定是等边三角形。 这一定理可以等价描述为:若以任意三角形的各边为底边向形外作底角为60°的等腰三角形,则它们的中心构成一个等边三角形。 一些引申: 1)四边形上,类似的定理为凡·奥贝尔定理。 2)拿破仑定理本身为佩特诺-伊曼-道格拉斯定理的特例。 3)内拿破仑三角形的面积大于等于 0 给出外森比克不等式。 10.莫利(Morley)定理:将三角形的三个内角三等分,靠近某边的两条三分角线相交得到一个交点,则这样的三个交点可以构成一个正三角形。这个三角形常被称作莫利正三角形。 (题外话:听高中同学说,某老师在外边上课给纯良的男孩纸们讲:跟喜欢的女孩纸说随便画一个三角形,如果它的角三分线交点恰好是正三角形,就证明对她的爱是真心的。我向那个高中同学当即表示,这就是红果果的欺骗啊~现在终于明白为什么自己还在汪汪汪了~~~) 11.欧拉线定理:任意三角形的外心、重心、垂心、九点圆圆心,依次位于同一直线上。(这条直线就叫三角形的欧拉线,且外心到重心的距离等于垂心到重心距离的一半) 12.沢山定理:圆P与圆O的内接四边形ABCD的对角线AC、BD切于E、F,同时与圆O相切,则E、F与△ABD、△ACD的内心I、I'共线(四点共线)。 二.初等代数篇 1.欧拉公式:(出于对欧拉大神的无比景仰崇拜以及对这个公式特有的赞赏,答主一定要把它先放出来,不过对大家来讲也许太熟悉了~) 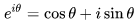 ,由此有一个经常被称作所谓“上帝公式”的恒等式(得名源于将五个基本常数汇聚一堂): ,由此有一个经常被称作所谓“上帝公式”的恒等式(得名源于将五个基本常数汇聚一堂): 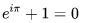 2.(i)对于任意的自然数n, 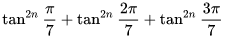 的值都是一个正整数。 的值都是一个正整数。 (ii)对于任意的自然数n, 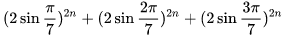 能被 能被 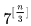 整除。 整除。 三.组合数学篇 1.对于简单多面体。设V为顶点数,E为棱数,F是面数,则 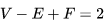 。 。 对任意的平面图,欧拉公式可以推广为: 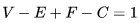 ,其中C为图中连通分支数。 ,其中C为图中连通分支数。 对非平面图,欧拉公式可以推广为:如果一个图可以被嵌入一个流形M,则: 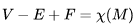 , , 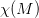 是此流形的欧拉示性数,在流形的连续变形下是不变量。单连通流形(例如球面或平面)的欧拉特征值是2。 是此流形的欧拉示性数,在流形的连续变形下是不变量。单连通流形(例如球面或平面)的欧拉特征值是2。 2.正多面体只有五种:正四面体、正六面体(正方体)、正八面体、正十二面体和正二十面体。 四、数学分析篇 1. 调和级数是发散的,然而: 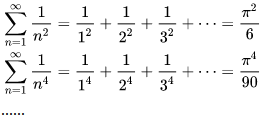 其实这些都是所谓的Riemann zeta function的特例,这个函数定义如下: 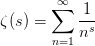 回到这部分开始给出的两个等式,用Zeta函数的形式就分别为 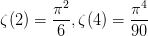 事实上,我们还有 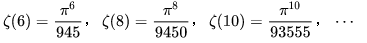 嗯,聪明的你一定会想到,肯定有个统一的公式!!好的,奖励你一颗糖,哦不,一个公式: 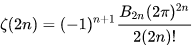 式中的 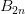 是偶数项的Bernoulli数(每一项都是有理数,n>1的奇数n项均为0,其余请自行学习Bernoulli number),总的来讲结果很美丽。如果你还知道生成函数概念的话,下面的结论希望你喜欢: 是偶数项的Bernoulli数(每一项都是有理数,n>1的奇数n项均为0,其余请自行学习Bernoulli number),总的来讲结果很美丽。如果你还知道生成函数概念的话,下面的结论希望你喜欢: 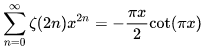 被惊艳到了有木有!!可是对于奇数的s,就没有这样漂亮的结果了,举个还算能看的例子: 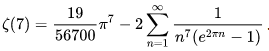 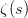 这个函数实在是包罗万象,十分迷人,许多很好的性质和漂亮的结论(上面的结果就是),甚至对于s=-1时,还有以下这个著名的等式: 这个函数实在是包罗万象,十分迷人,许多很好的性质和漂亮的结论(上面的结果就是),甚至对于s=-1时,还有以下这个著名的等式: 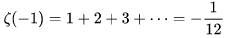 特别说明,s=-1时的情况是解析延拓意义下的,上面这个式子的等号的含义也和我们通常熟知的情形不同,然而大部分人看过的所谓的加加减减的证明更是民科之至,当作个好玩的东西就可以了,那种证明是错误的,为了不偏题太远,不展开说了。它的一般结果为: 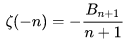 由Bernoulli数的性质就有 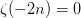 还有更多奇妙的性质,大家自行去wiki吧,哈哈~(复变函数简直打开了新世界的大门~~) 五、数论篇 1. Fermat大定理推广形式的恒等式:(以勾股定理为[2,2]型,Fermat大定理为[2,n]型为例) (1). [3,3]型: 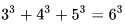 (2). [4,4]型: 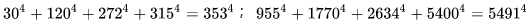 (3). [4,5]型: 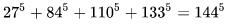 (4). [5,5]型: 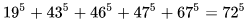 (5). [7,7]型: 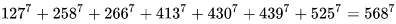 (6). [8,8]型: 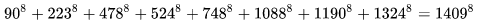 (7). [3,4]型:(无穷多个,太大就不写在下面了,反正也不够漂亮了) 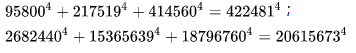 2. 整幂次和的其他恒等式: (1). Euler四平方和恒等式及Lagrange的四平方和定理:前者的表述为“如果两个数都能表示为四个平方数的和,则这两个数的积也能表示为四个平方数的和。”后者则为“每一个正整数都可以表示为四个平方数之和。” (2).Brahmagupta-Fibonacci定理: 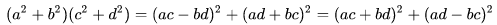 例如: 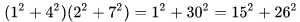 (3). 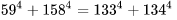
「关于」立创商城成立于2011年,致力于为客户提供一站式电子元器件线上采购服务,成交量全国领先。拥有10000多平方米现代化元器件仓库,现货库存超150000种。本文由立创商城整合,版权归原作者所有。
|