ECC算法介绍
ECC（Elliptic Curves Cryptography）加密算法是⼀种公钥加密算法，与主流的RSA算法相⽐，ECC算法可以使⽤较短的密钥达到
相同的安全程度。近年来，⼈们对ECC的认识已经不再处于研究阶段，开始逐步进⼊实际应⽤，如国家密码管理局颁布的SM2算法就是基
于ECC算法的。下⾯我们来认识⼀下ECC的⼯作原理。
椭圆曲线
定义
在引⼊椭圆曲线之前，不得不提到⼀种新的坐标系-------射影平⾯坐标系，它是对笛卡尔直⾓坐标系的扩展，增加了⽆穷远点的概念。
在此坐标系下，两条平⾏的直线是有交点的，⽽交点就是⽆穷远点。两者的变换关系为：
笛卡尔坐标系中的点a（x,y），令x=X/Z，y=Y/Z，则射影平⾯坐标系下的点a的坐标为（X,Y,Z)，如点（2,3）就转换为（2Z,3Z,Z）。
椭圆曲线定义：⼀条椭圆曲线在射影平⾯上满⾜⽅程：
的所有点的集合，且曲线上每个点都是⾮奇异的。
该⽅程有名维尔维斯特拉斯⽅程，椭圆曲线的形状不是椭圆，只是因为其描述的⽅程类似于计算⼀个椭圆周长的⽅程。转换到笛卡尔坐标系
下的⽅程为：
|
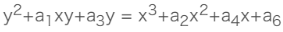
楼主
标题置顶
标题高亮
