|
CRC 即循环冗余校验码（Cyclic Redundancy Check）：数据通信领域中最常用的一种差错校验码，其信息字段和校验字段长度可以任意指定，但要求通信双方定义的 CRC 标准一致。 一、CRC 算法原理对于工控领域，我们主要利用 CRC 校验来处理各种数据流的数据正确性校验。 CRC 算法原理：在 K 位信息码（目标发送数据）后再拼接 R 位校验码，使整个编码长度为 N 位，因此这种编码也叫（N,K）码。通俗的说，就是在需要发送的信息后面附加一个数（即校验码），生成一个新的发送数据发送给接收端。这个数据要求能够使生成的新数据被一个特定的数整除。 那么，CRC 校验的具体做法就是： （1）选定一个标准除数（K 位二进制数据串）； （2）在要发送的数据（m 位）后面加上 K-1 位 0，然后将这个新数（M+K-1 位）以模 2 除法的方式除以上面这个标准除数，所得到的余数也就是该数据的 CRC 校验码（注：余数必须比除数少且只少一位，不够就补 0）； （3）将这个校验码附在原 m 位数据后面，构成新的 M+K-1 位数据，发送给接收端； （4）接收端将接收到的数据除以标准除数，如果余数为 0 则认为数据正确。 注意：CRC 校验中有两个关键点：一是要预先确定一个发送端和接收端都用来作为除数的二进制比特串（或多项式）；二是把原始帧与上面选定的除数进行二进制除法运算，计算出 FCS（Frame Check Sequence，帧校验序列）。多项式可以随机选择，也可按国际上通行的标准选择，但最高位和最低位必须均为“1”。 例如，对于数据 10110011，以指定除数 110011 求它的 CRC 校验码，其过程如下： [color=var(--theme-color)]
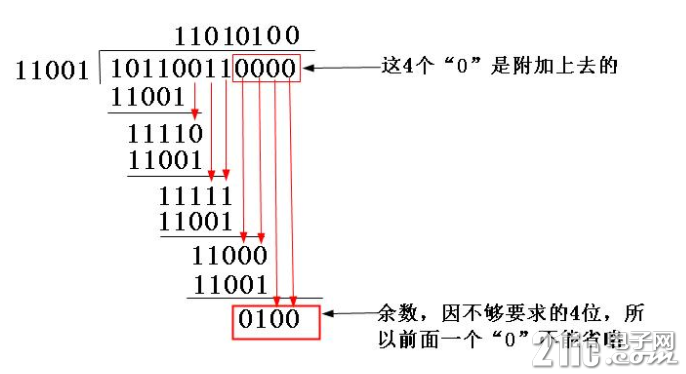
注：模 2 除法，或者叫二进制除法，实际上也就是异或运算。 二、CRC 算法的几个概念单纯谈 CRC 的模 2 除法其实并不困难，但实际计算中经常会遇到计算出来的结果和实际不一致的情况，这也是这几天我在看的东西。 这里需要知道几个组成部分或者说计算概念：多项式公式、多项式简记式、数据宽度、初始值、结果异或值、输入值反转、输出值反转、参数模型。 2.1 多项式公式对于 CRC 标准除数，一般使用多项式（或二项式）公式表示，如上例中除数 11011 的二项式为 G(X)=X4+X3+X+1，X 的指数就代表了该 bit 位上的数据为 1,（最低位为 0）。这里特别注意一下位数问题，除数的位数为二项式最高次幂+1（4+1=5），这个很重要。 2.2 多项式简记式通过对 CRC 的基本了解我们知道，多项式的首尾必定为 1，而这个 1 的位置在下一步计算一定为 0，所以就把前面这个 1 给省略掉了，出现了一个叫简记式的东西，如上例中除数 11011 的简记式为 1011，很多看过 CRC 高级语言源码的人会知道，对于 CRC_16 标准下 G(X)=X16+X15+X2+1（16#18005）的 poly 值实际上是 8005，这里使用的就是简记式。后面会对这个用法做一个说明。 2.3 数据宽度数据宽度指的就是 CRC 校验码的长度（二进制位数），知道了 CRC 的运算概念和多项式，就可以理解这个概念了，CRC 长度始终要比除数位数少 1，与简记式长度是一致的。 以上三个数据就是我们经常能够用到的基本数据。 2.4 初始值与结果异或值在一些标准中，规定了初始值，则数据在进行上述二项式运算之前，需要先将要计算的数据与初始值的最低字节进行异或，然后再与多项式进行计算。 而在结果异或值不为零的情况下，则需要将计算得到的 CRC 结果值再与结果异或值进行一次异或计算，得到的最终值才是我们需要的 CRC 校验码。 这里可以看出，初始值与结果值的位数要求与数据宽度一致。 2.5 输入值反转与输出值反转输入值反转的意思是在计算之前先将二项式反转，然后再用得到的新值和数据进行计算。如对于 G(X)=X16+X15+X2+1（16#18005），其正向值为 1 1000 0000 0000 0101，反转值则为 1010 0000 0000 0001 1 输出值反转则是将最终得到的 CRC 结果反转。 通常，输入值反转后的结果值也会是反转的，所以这两个选项一般是同向的，我们只有在在线 CRC 计算器中会看到自由选择正反转的情况存在。 那么，这里引用一段总结： CRC16、CRC32 等多字节的校验值的计算有几点需要清楚（只针对一次一个字节的算法）： 1) 初始值不为 0 的情况下，该如何计算： 输入数据需要反转时：先将要计算的数据与初始值的最低字节进行异或，再与反转后的多项式进行计算。 输入数据不需要反转时：先将要计算的数据左移到与初始值对齐的位置（如 CRC16 算法，则左移 8 位，低位填充 0；如 CRC32 算法，则左移 24 位，低位填充 0）与初始值进行异或，再与正常的多项式进行计算。 2) 结果异或值不为 0 的情况：第一步算得到的 CRC 值再与结果异或值进行异或操作得到最终的校验值： 输出数据反转：如果输入数据是反转的模式，则结果也是反转的 输出数据不反转：如果输入数据是不反转的模式，则结果也是不反转的 3）初始值的选择是可自己定义，很多不同的厂家使用的初始值是不一样，不一样的初始值得到的结果也是不一样的。 不同的二项式、初始值、结果异或值、反转原则都会造成最终的结果不一致，这就是为什么明明是正确的计算方式，有时候算出来的结果却总是不正确。 那么，如何去判断应该采用哪些原则呢？这里谈到最后一个概念： 6、参数模型 虽然 CRC 可以任意定义二项式、数据长度等，但没有一个统一的标准的话，就会让整个计算变得非常的麻烦。但实际上，不同的厂家经常采用不同的标准算法，这里列出了一些国际常用的模型表： [color=var(--theme-color)]
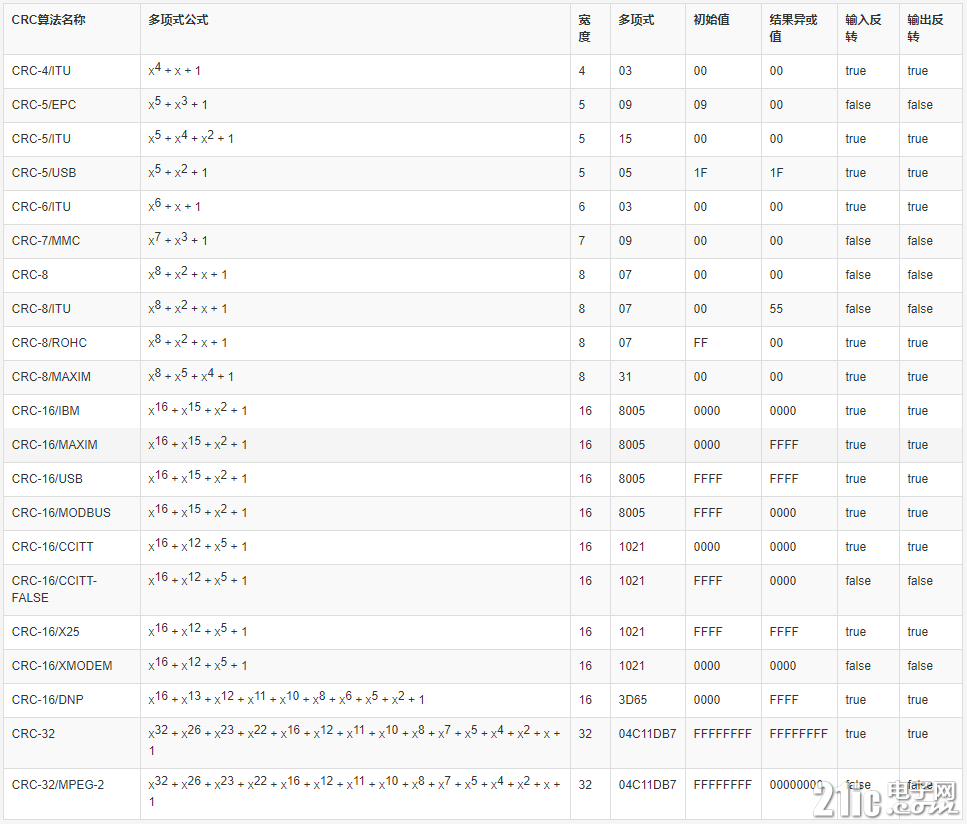三、CRC 算法实例理解了 CRC 算法的原理和几个概念之后，接下来看一下 CRC 算法实例。使用 CRC-8 算法求 101001110100001 的效验码。CRC-8 标准的 h(x) = x^8 + x^7 + x^6 + x^4 + x^2 + 1，既 h(x)是 9 位的二进制串 111010101。 [color=var(--theme-color)]
经过迭代运算后，最终得到的 r 是 10001100，这就是 CRC 效验码。 通过示例，可以发现一些规律，依据这些规律调整算法： （1）每次迭代，根据 gk 的首位决定 b，b 是与 gk 进行运算的二进制码。若 gk 的首位是 1，则 b=h；若 gk 的首位是 0，则 b=0，或者跳过此次迭代，上面的例子中就是碰到 0 后直接跳到后面的非零位。 [color=var(--theme-color)]
（2）每次迭代，gk 的首位将会被移出，所以只需考虑第 2 位后计算即可。这样就可以舍弃 h 的首位，将 b 取 h 的后 m 位。比如 CRC-8 的 h 是 111010101，b 只需是 11010101。 [color=var(--theme-color)]
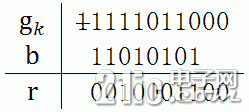
（3）每次迭代，受到影响的是 gk 的前 m 位，所以构建一个 m 位的寄存器 S，此寄存器储存 gk 的前 m 位。每次迭代计算前先将 S 的首位抛弃，将寄存器左移一位，同时将 g 的后一位加入寄存器。若使用此种方法，计算步骤如下： [color=var(--theme-color)]
注：蓝色表示寄存器 S 的首位，是需要移出的，b 根据 S 的首位选择 0 或者 h。黄色是需要移入寄存器的位。S’是经过位移后的 S。 四、CRC 算法的 C 语言实现根据上述分析的 CRC 算法规律，可以总结 C 语言实现步骤如下： （1）设置 CRC 寄存器，并给其赋值为“余数初始值”。 （2）将数据的第一个 8-bit 字符与 CRC 寄存器进行异或，并把结果存入 CRC 寄存器。 （3）CRC 寄存器向左移一位，LSB 补进一位数据，移出并检查 MSB。 （4）如果 MSB 为 0，重复第三步；若 MSB 为 1，CRC 寄存器与 0xD5 相异或。 （5）重复第 3 与第 4 步直到 8 次移位全部完成。此时一个 8-bit 数据处理完毕。 （6）重复第 2 至第 5 步直到所有数据全部处理完成。 （7）最终 CRC 寄存器的内容即为 CRC 值（部分结果需要异或或者取反，视情况而定，见 2.6 小节）。 #define POLY 0xD5
/**
* Calculating CRC-8 in 'C'
* [url=home.php?mod=space&uid=118580]@para[/url] addr, start of data
* @para num, length of data
* @para crc, incoming CRC
*/
uint16_t crc8(unsigned char *addr, int num, uint8_t crc)
{
int i;
for (; num > 0; num--) /* Step through bytes in memory */
{
crc = crc ^ (*addr++ << 8); /* Fetch byte from memory, XOR into CRC top byte*/
for (i = 0; i < 8; i++) /* Prepare to rotate 8 bits */
{
if (crc & 0x80) /* b7 is set... */
crc = (crc << 1) ^ POLY; /* rotate and XOR with polynomic */
else /* b7 is clear... */
crc <<= 1; /* just rotate */
} /* Loop for 8 bits */
crc &= 0xFF; /* Ensure CRC remains 8-bit value */
} /* Loop until num=0 */
return(crc); /* Return updated CRC */
}
示例性的 C 代码如上所示，因为效率很低，项目中如对计算时间有要求应该避免采用这样的代码。这个代码有一个 crc 的参数，可以将上次计算的 crc 结果传入函数中作为这次计算的初始值，这对大数据块的 CRC 计算是很有用的，不需要一次将所有数据读入内存，而是读一部分算一次，全读完后就计算完了。这对内存受限系统还是很有用的。
| 
楼主
标题置顶
标题高亮
