|
回忆特征点法中,由于我们通过匹配描述子,知道了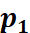 , , 的像素位置,所以可以计算重投影的位置。但在直接法中,由于没有特征匹配,我们无从知道哪一个 的像素位置,所以可以计算重投影的位置。但在直接法中,由于没有特征匹配,我们无从知道哪一个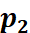 与 与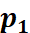 对应着同一个点。直接法的思路是根据当前相机的位姿估计值,来寻找 对应着同一个点。直接法的思路是根据当前相机的位姿估计值,来寻找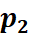 的位置。但若相机位姿不够好, 的位置。但若相机位姿不够好,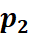 的外观和 的外观和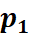 会有明显差别。于是,为了减小这个差别,我们优化相机的位姿,来寻找与 会有明显差别。于是,为了减小这个差别,我们优化相机的位姿,来寻找与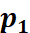 更相似的 更相似的 。这同样可以通过解一个优化问题,但此时最小化的不是重投影误差,而是光度误差(Photometric Error),也就是P的两个像的亮度误差: 。这同样可以通过解一个优化问题,但此时最小化的不是重投影误差,而是光度误差(Photometric Error),也就是P的两个像的亮度误差: 
注意这里e是一个标量,所以没有加粗。同样的,优化目标为该误差的二范数,暂时取不加权的形式,为: 
能够做这种优化的理由,仍是基于灰度不变假设。在直接法中,我们假设一个空间点在各个视角下,成像的灰度是不变的。我们有许多个(比如N个)空间点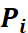 ,那么,整个相机位姿估计问题变为: ,那么,整个相机位姿估计问题变为: 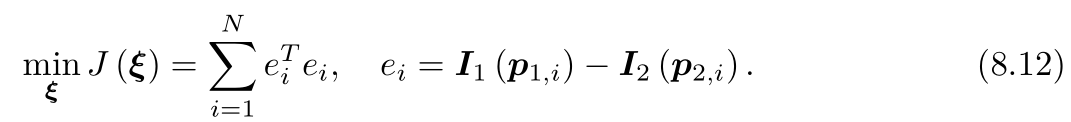
注意这里的优化变量是相机位姿ξ 。为了求解这个优化问题,我们关心误差e是如何随着相机位姿变化的,需要分析它们的导数关系。因此,使用李代数上的扰动模型。我们给exp(ξ) 左乘一个小扰动exp(δξ) ,得: 
类似于上一章,记 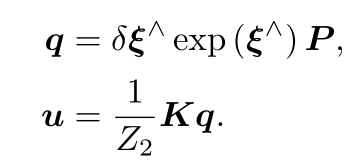
这里的q为P在扰动之后,位于第二个相机坐标系下的坐标,而u为它的像素坐标。利用一阶泰勒展开,有: 
我们看到,一阶导数由于链式法则分成了三项,而这三项都是容易计算的: 1.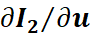 为u 处的像素梯度; 为u 处的像素梯度; 2.  为投影方程关于相机坐标系下的三维点的导数。记 为投影方程关于相机坐标系下的三维点的导数。记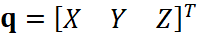 ,根据上一节的推导,导数为: ,根据上一节的推导,导数为: 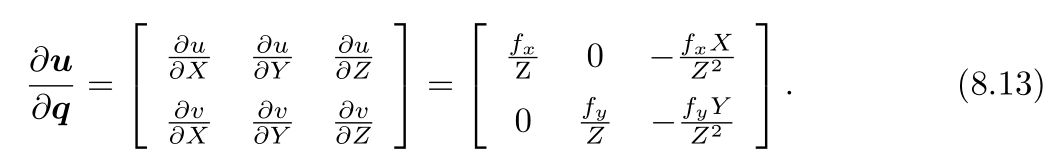
3. 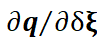 为变换后的三维点对变换的导数,这在李代数章节已经介绍过了: 为变换后的三维点对变换的导数,这在李代数章节已经介绍过了: 
在实践中,由于后两项只与三维点q有关,而与图像无关,我们经常把它合并在一起: 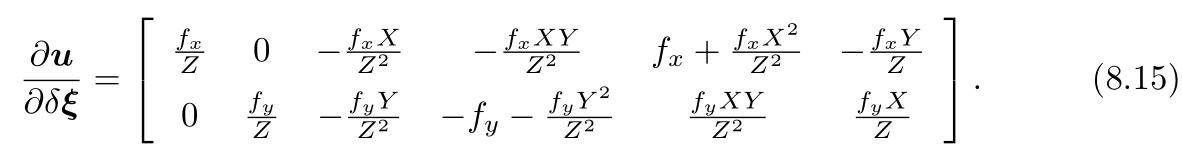
这个2×6的矩阵在上一讲中也出现过。于是,我们推导了误差相对于李代数的雅可比矩阵: 
对于N个点的问题,我们可以用这种方法计算优化问题的雅可比,然后使用G-N或L-M计算增量,迭代求解。至此,我们推导了直接法估计相机位姿的整个流程,下面我们通过程序来演示一下直接法是如何使用的。
|