本帖最后由 jonas222 于 2025-1-25 22:58 编辑
插值算法是一种很常用的数据处理手段,插值包括了最邻近插值、线性插值(单线性和双线性)、样条插值(自然样条、抛物样条),本文以抛物样条和自然样条两种方法进行对比,基于ARM单片机GD32F103进行测试。 测试函数 - #include "dsp_test.h"
- static arm_spline_instance_f32 S; //样条插值结构体
- static arm_spline_type type=ARM_SPLINE_NATURAL; //自然样条插值
- static float32_t x[32]; //原始数据x
- static float32_t y[32]; //原始数据y
- static uint32_t n=32; //原始数据个数
- static float32_t coeffs[3*(32-1)]; //稀疏矩阵
- static float32_t tempBuffer[2*(32-1)]; //内部计算缓冲数组
- static float32_t xq[128];
- static float32_t pDst[128];
- static uint32_t blockSize=128;
- #define num_tab 128/32
- void interp_test(u8 mode)
- {
- if(mode)
- {
- type=ARM_SPLINE_NATURAL;//自然样条插值
- }
- else
- {
- type=ARM_SPLINE_PARABOLIC_RUNOUT;//抛物样条插值
- }
- u8 i=0;
- for(i=0;i<32;i++)
- {
- x[i]=i*num_tab;
- y[i]=1.f+arm_sin_f32(100.f*PI*i/256.f+PI/3.f);
- }
- for(i=0;i<128;i++)
- {
- xq[i]=i;
- }
- arm_spline_init_f32(&S,type,x,y,n,coeffs,tempBuffer);
- arm_spline_f32(&S,xq,pDst,blockSize);
- printf("*****x********\r\n");
- for(i=0;i<32;i++)
- {
- printf("%f\r\n",x[i]);
- }
- printf("*****y********\r\n");
- for(i=0;i<32;i++)
- {
- printf("%f\r\n",y[i]);
- }
- printf("*****x1********\r\n");
- for(i=0;i<128;i++)
- {
- printf("%f\r\n",xq[i]);
- }
- printf("*****y1********\r\n");
- for(i=0;i<128;i++)
- {
- printf("%f\r\n",pDst[i]);
- }
- }
测试结果 [backcolor=var(--bg3)]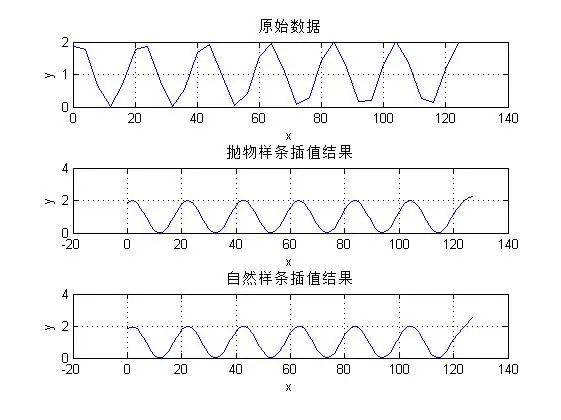
样条插值测试结果 可以看出插值后,正弦曲线变得很平滑,两者插值在细节上 无明显的区别,,只是最后几个点和趋势上抛物样条插值变缓 自然样条插值保持跟原始数据一样
|