用VNA学习PDN电源完整性

NanoVNA大家应该早拿到手了，现在用这个仪器学习PDN电源完整性。

使用仪器，记得经常校准！！


先测量个200Ω电阻：




表上显示低频阻抗是200Ω：

再连接一个270pF电容=





用随机附带的连接线，连接到电脑USB，然后打开软件，看串联电容：







这个是显示的特性曲线！






然后用鼠标点击曲线上任意一点，就可以看到该频率点下的等效串联LC和并联RX等众多参数。







黑白电视机上标称56uH的功率电感：

关于理想电容、电感和电阻的频率特性，在log-log频率特性曲线上，电容的斜率是-1，电感的斜率是+1，电阻是0：







注：图中仿真器仿真电路中，加了个1GΩ电阻，因为仿真器要求每个节点都要直流通路到地，否则会“生气”，所以每个电路都加1GΩ电阻。



对于实际电容器，例如我们上面测的270pF电容，只是在9MHz以内，斜率是-1：






而功率电感只是到3M范围内呈感性：

关于幅度和相位的关系，一般读者直接记住相关结论就行了，例如极点处，相位下降45°等。

有的PDN书籍比较“惹事”，就幅度和相位之间的约束关系，提到了K-K关系：


这就牵扯到了希尔伯特变换，对于电工来说，这个话题就太难了。

切换看问题的角度，可以让读者对“老”问题，产生更深刻的认识，所以，即便读者已经熟悉频率响应、波特图的画法，既然扯到了希尔伯特变换，那么我们就换个角度看老问题。


先复习一下增益和相位的定义：





针对上面的这个复数，由希尔伯特变换联系起实部和虚部之间的关系：






那么对于某个具体传递函数，例如H(S)=1+S


其增益为：





图中蓝线为理想的半无穷斜坡增益，红线为实际增益。

使用希尔伯特变换，对增益曲线进行积分，可得相位曲线：

据此，我们得到了最基本的增益相位曲线：







然后对上面曲线，使用移位、尺度变换、反相等技术，可得其它各种可能的增益相位曲线，而无需再一一套用希尔伯特变换。


例如倘若增益曲线的斜率=1/2，则：







如果增益曲线下移：







如果斜率为-1：







如果增益曲线右移a单位：

学习模拟电路，必然要懂频率响应，尤其是波特图的画法。
如果不愿意接受希尔伯特变换，那么必须死记硬背电路原理或电路分析基础教科书上的结论，把传递函数的分子和分母分成N种类型，然后研究每种类型下的波特图特点。
而且零极点有标准零极点形式和颠倒的形式之分：



如此一来，要背诵十几种零极点的波特图特点。

而倘若能理解希尔伯特变换，就无需这么痛苦了，当然了，代价是花点时间理解这个变换。

根据希尔伯特变换对，可知对于最小相位系统，有两个结论：
①某个区域的相位，大致上是正比于该区域增益曲线的斜率；
②如果增益只是在jw轴上有限区域内变化，那么在恒定区域的相位，大致上反比于和该区域的之间的距离。


关于第②点的示例：




关于第①点的示例：





上图中粉色箭头处，增益的斜率为无穷大，所以对应频率点处的相位也趋于无穷大，且第一个箭头处是＋∞，第二个箭头处是-∞
对于恒定增益处变化趋势，套用第①个结论。




据此，给定增益曲线，根据上面两个结论，可以迅速判断出相位曲线的大致形状！！！

有人可能好奇，为何要对传递函数取对数？这是几个意思？






这就是数学的魅力问题了。
数学家喜欢对某一大类型问题研究，看看它们共同的数学特征是什么。
在静电学、静磁学问题中，电/磁标量势的共同特点，是位置的函数，相关函数的标量值可以写成P（x,y，z)的形式。
也就是说如果标量函数的函数值，只是其独立变量的函数，这种函数叫状态函数，状态函数中有个特殊情形，叫势函数！！
势函数是电路原理的根基！电路理论中很多东西都是直接从势函数理论借来的，或类比来的。
状态函数有个特征，就是有全微分：





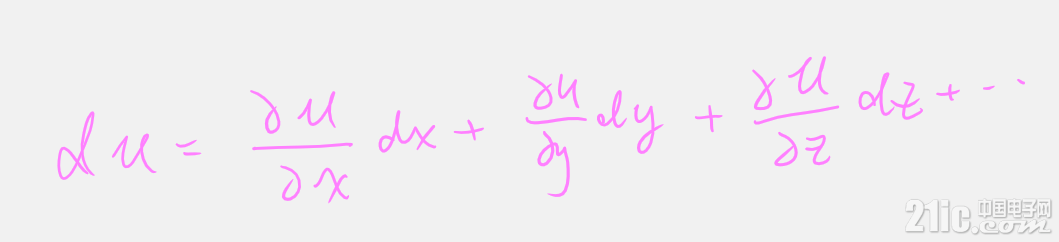
状态函数的特殊情形  ---势函数，不但有上面的全微分，还满足拉普拉斯方程：







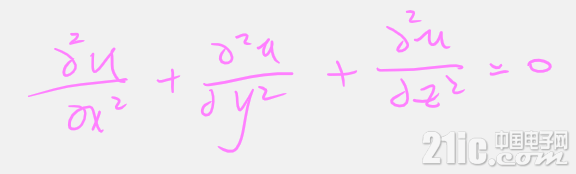
对于三维牛顿势函数，得到是重力论。
而对于二维或对数势函数，刚好和电路理论必须的--复变量理论靠近！！！







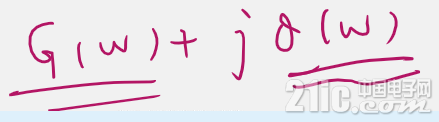
上式是复数！！所以电路理论中主要研究对数势函数！复变理论的结论可以直接拿过来用了。


这就是为何对传递函数取对数的原因！！！


除了对数增益，电路理论中还有个对数插入传输函数，那里也要取对数，进而转换成复数理论研究。

实践类的内容，比较简单轻松，至少比学习严谨、逻辑性极强的理论要容易一点。
至少，算不出来的东西，就不算了，而是直接测试，也就是说可以耍赖皮



静电屏蔽


如下图所示，有两个平行导体A和B，图中给出的是横截面示意图：






既然是静电分析，静电能是储存在电容中的，所以借助于电容，可以轻松地分析出静电场问题。
于是问题由场，切换到简单的电路问题了。






如果A导体上有个脉冲电压V，那么导体B上的噪声电压Vn是分压公式：






如果在A和B之间加一个导体片，这又可以分成两种情形：

一、导体片接地

假设导体片加在AB中间，那么此时电容Cc2=2Cc1，因为距离减倍了：





如果所加的导体面能把A包的严严实实，理论上Vn=0，即一点噪声也传不到B导体上。


可惜，实践中做不到这么理想，必然有个或大或小的空隙，能让噪声传到B上，这里用电容Cs建模：







此时等效电路模型为：





这个结果和上面结果比较，分子Cs<<Cc1，而分母比上面公式的分母大，所以结果是噪声电压大大减小了。




二，导体片不接地

如下图，此时相当于两个电容Cc2串联，所以等效电容=Cc2/2




和结果1比较，结果完全相同，也就是说，如果屏蔽层不接地，没有屏蔽效果！！！


但是，这个结论成立的前提是屏蔽板和地之间没有电容！！！


实际上这是不可能的！！！！


考虑到屏蔽板和地之间 的电容Cp，等效电路为：






可见，如果极板面积比较大，Cp会比较大，那么和第一个结果相比较，即便屏蔽板没有接地，也可以大大减低噪声Vn

如果一切都是理想的，那么人类起码可以进步100年，屏蔽也变的小儿科了：







如上图，如果屏蔽层中没有电流流动，屏蔽效果是理想加完美的！！！


可惜的是，实际上是不可能的！所以我们必须进一步分析实际情形,所以故事才刚刚开始！！！

不错，