本帖最后由 xukun977 于 2020-3-27 20:55 编辑
下面推导带电杂质引起的散射,给出著名的卢瑟福散射公式!
有一电子,带有负电荷-q,离子化施主为+q,电子入射速度为v0,距离+q的垂直距离为b:
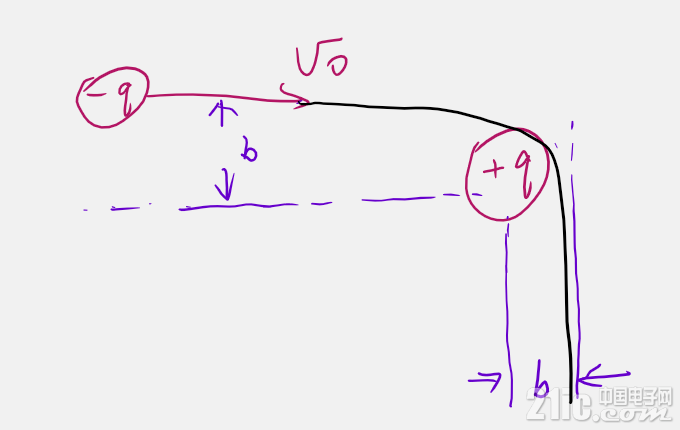
当电子入射速度非常慢时,电子有个指向+q的加速度,大小反比于和施主之间的距离的平方!偏转角度达到最大,如上图所示,最终轨迹渐进线距离+q也是b。
对于更慢的电子,其轨迹的偏转角度是多少?
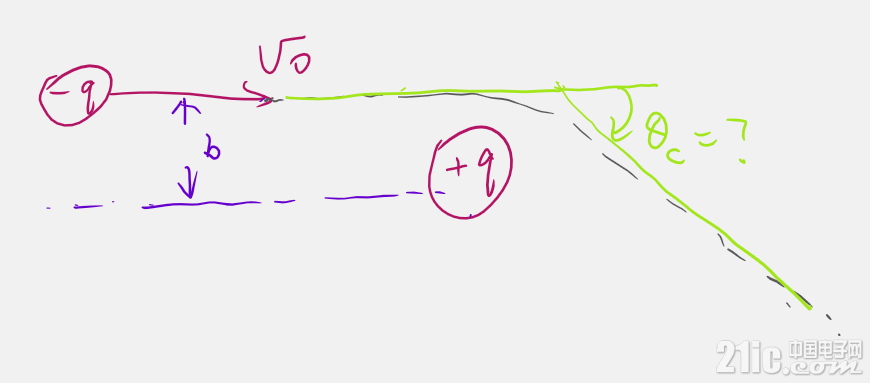
首先建立坐标,坐标原点位于+q施主处,分别建立x-y平面和极坐标r/_θ

根据牛顿定律和洛伦兹力方程,有:
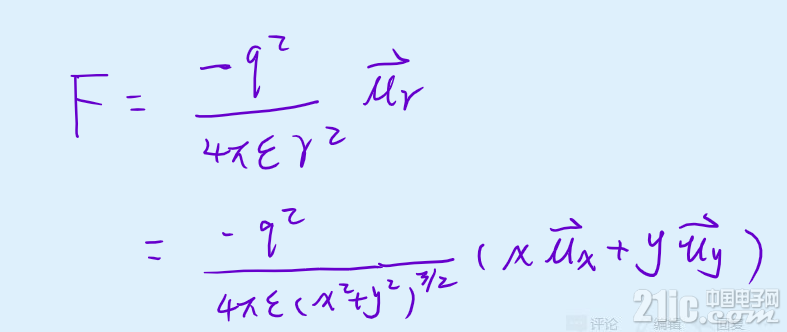
式中的u为单位矢量,上面有个箭头。
对x分量使用牛顿定律:

上式中,已由直角坐标转换为极坐标。
因为x,y轴的选择是任意的,所以上面方程必须与这个选择无关!!!!!
要想满足这个要求,必然有:

即一个方程,转换成两个方程了,用模拟版块某些人的话说,可以把"鬼画符"变成“”精美公式“:


(编辑公式没问题,就是有点耗费时间)
下面来看上面两个方程是什么意思。
对于第一个方程,可等价表示成:

注意括号中项,物理学中定义为角动量!!!
角动量的导数为零,意思是角动量要守恒!!!!!!!
既然角动量要守恒,那么电子的初始角动量是多少?
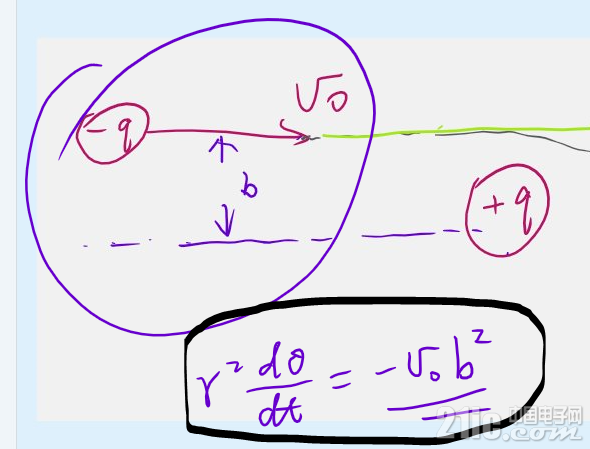
把这个初始角动量代入第二个方程,可得:

|