本帖最后由 catnull 于 2021-8-30 18:55 编辑
一、引言
很幸运申请到了南京沁恒自主设计的RISC-V内核CH32V103R8T6。它有72Mhz的系统主频，SRAM有20KB, FLASH有64KB也是够用了。开发板很精致，也设置了Arduino的接口，方便使用一些Arduino接口板开发板。上面自带了一个WCH-LINK 下载仿真器，可以很方便的进行程序的调试。片上丰富的资源，可以展开DSP的实验，特别是离散傅里叶变换的实验。这种数字信号处理的应用相当广泛，例如一些市面上的调音器，还有心率识别，等等，都可以使用傅里叶变化对时域信号进行处理，之后变成频域信号。
二、思路简介
网络上已经有了STM32官方的快速傅里叶变换的库了，相关的应用也开展了不少。但是咱们的CH32V103行不行？直接移植过来，因为涉及到底层的运算优化，非我的能力所能达到。但是作为实验的题目，先解决零到壹的问题。从无到有来解决最好了。
后面找到一本数字信号的书，名字叫做《实用数字信号处理——从原理到应用》， Digital Signal Processing A Practical Guide for Engineers and Scientists , 是一个美国人写的， Steven W. Smith。由北航的两位老师翻译成中文。认真读了一番，因为之前数学上恶补了关于傅里叶变换的知识，啃下了物理系的《数学物理方法》中的复变函数论，所以读起来还算有所收获。
参考里面的BASIC程序，我移植为C语言。先在QT上调试了一番，后面移植到了开发板上，算是达到能用的水平。
但是特别提醒一点，需要打开MountainRiver山河编译器里面的一些编译选项，才能支持数学库里面的正弦余弦运算，以及浮点数的模拟运算的功能（RISC-IMAC是没有实现浮点指令集的，浮点运算需要模拟为整数进行）。
打钩用于一些浮点数的输入输出，方便调试。
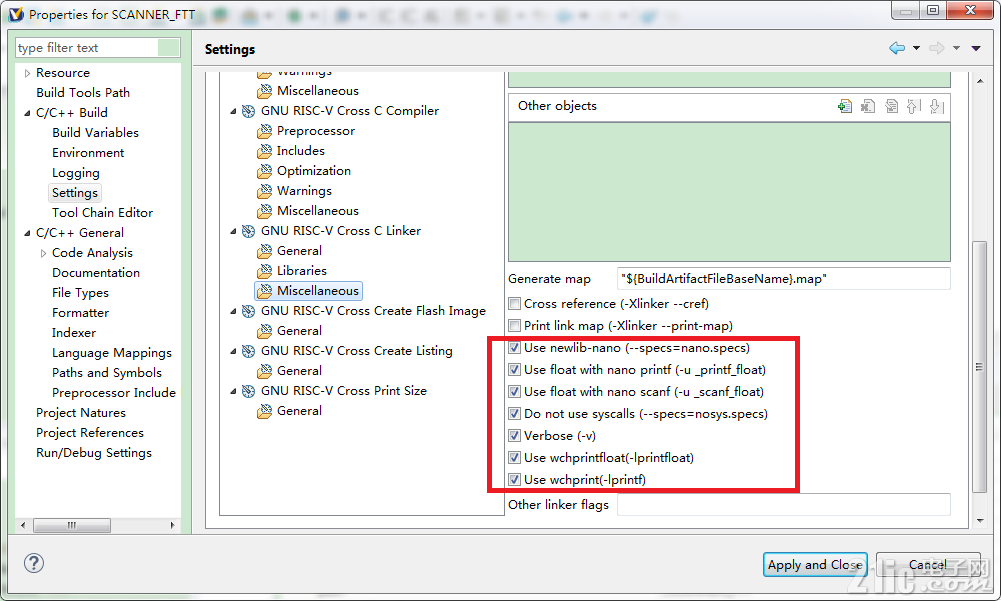
下图中的m 编译时时 gcc会加上 -lm，会调用数学库。没有加的或无法计算正余弦函数。
3、快速傅里叶变换FFT库文件中的代码
具体的代码如下：
头文件： cr2_fft.h
/******************
*
* Fast Fourier Transformer
*
* Author : 张远东 莆田 seighbang@126.com
*
*
********************/
#ifndef CR2_FFT_H
#define CR2_FFT_H
#define PI 3.14159265
#define FFT_N 1024
typedef struct complex
{
float real ;
float imag ;
} complex;
int fft(complex* x);
int ifft(complex* x );
#endif // CR2_FFT_H
#include "cr2_fft.h"
#include <math.h>
int fft(complex* x)
{
int i =0;
int ip = 0;
int j = 0;
int jm1 = 0;
int k = 0;
int l = 0;
int le = 0;
int le2 = 0;
int nm1 = FFT_N-1;
int nd2 = FFT_N/2;
int m = (int)(log(FFT_N)/log(2));
complex t = {.real = 0.0, .imag = 0.0};
complex u = {.real = 1.0, .imag = 0.0};
complex s = {.real =0.0, .imag = 0.0};
/*bit reversal sorting of x_in*/
j = nd2;
for(i = 1; i < nm1; i ++)
{
if(i < j) // while the i < j , transverse x[i],x[j],
{
t=x[i];
x[i] = x[j];
x[j] = t;
}
//Rather mechod to bit reverse arrangement
k = nd2;
while(k <= j)
{
j = j - k; //set the big end bit to 0
k = k/2; //the next bit , from up bit k to next bit k/2...
}
j = j + k; //set the big end bit to 1, as k > j
}
/******************************************************
*
* DFT routine
*
*******************************************************/
for(l =1 ; l <= m; l ++)
{
le = (int)(1<<l);
le2 = le/2;
u.real = 1.0;
u.imag = 0.0;
s.real = cos(PI/le2);
s.imag = -sin(PI/le2);
for(j = 1 ; j <= le2; j++) //for each sub DFT
{
jm1 = j -1;
for(i = jm1; i <= nm1; i = i + le) //loop for each Butterfly
{
ip = i + le2;
t.real = x[ip].real * u.real - x[ip].imag * u.imag;
t.imag = x[ip].real * u.imag + x[ip].imag * u.real;
x[ip].real = x[i].real - t.real;
x[ip].imag = x[i].imag - t.imag;
x[i].real = x[i].real + t.real;
x[i].imag = x[i].imag + t.imag;
}
t.real = u.real;
u.real = t.real * s.real - u.imag * s.imag;
u.imag = t.real * s.imag + u.imag * s.real;
}
}
return 0;
}
/********************************************************************************
*
* INVERSE FAST FOURIER TRANSFORM FUNCTION
*
********************************************************************************/
int ifft(complex * x)
{
int i = 0;
int k = 0;
int n = FFT_N ;
int nm1 = FFT_N - 1;
//change the sign of imag part of x[]
for( k = 0; k < n; k++)
{
x[k].imag = -x[k].imag;
}
//forward FFT
fft(x);
for(i = 0 ; i< n; i++) //divide the time domain by N and change the sign of x[].imag.
{
x[i].real = x[i].real/n;
x[i].imag = -x[i].imag/n;
}
return 0;
}
4. 测试样例：
SCANNER_FTT_2021_08_30.zip
(852.31 KB)
5. 测试的效果：
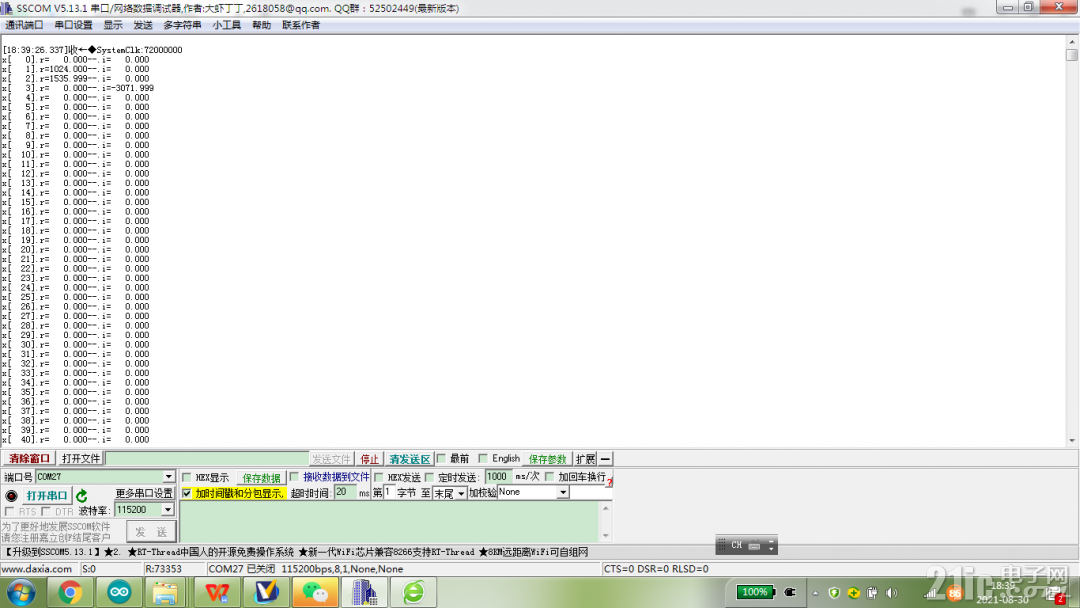
6.致谢： 感谢南京沁恒公司对我的厚爱，和沁恒的缘分很长，2014年做Arduino的板子，使用的是CH340G，之前也申请过CH32F103的开发板，沁恒也是支持。这次的比赛我也很幸运得到了开发板的物质支持。向沁恒的工程师们致敬！谢谢！
| 
楼主
标题置顶
标题高亮
