PID控制算法的简单分析和仿真！

发表于 2019-4-30 22:33

1、首先我们来看一下PID系统的基本组成模块：

如图所示，图中相关参数的表示如下：

r(t)：系统实际上需要的输出值，这是一个标准值，在我们设定了之后让这个系统去逼近的一个值（随时间变化的原因是，我们对系统的需求不同才会改变！）

y(t)：系统当前的输出值，这个值应该需要趋近于我们设定的值，当我们没有增加PID控制模块之前，它是由被控对象通过r(t)输入直接产生的。

e(t)：系统由于某些扰动，导致的系统产生的偏差，实际输出的值和想要设定的初始值r(t)的差值。

u(t)：系统通过PID控制器输出的新的输入值，实际上他是在r(t)的基础上，针对当前的实际情况做出的改变。

Kp比例模块：系统PID比例因子，Kp能够对于产生的偏差e(t)能够迅速的作出反应，减少偏差。

Ki积分模块：系统PID积分因子，Ki能够用于消除静差，由于前面的误差有正有负，所以当前偏差的加入能够抵消部分，保持系统的稳定性，让系统有**功能。

Kd微分模块：系统微分因子，Kd能够体现出当前误差的变化趋势，引入有效早期修正信号，从而加快系统的动作速度，减少调节时间。

图中所示的信号关系公式如下所示：

信号误差公式：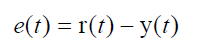

模拟信号的PID控制器公式：

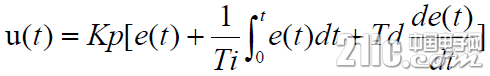
离散信号的PID控制器公式：

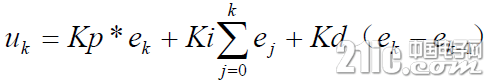
被控对象的信号公式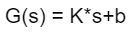：（简单的线性系统，比如电机的PWM调速系统）

上述公式参数描述：

Kp控制器比例系数、Ti控制器积分时间(积分系数）、Td控制器微分时间(微分系数）

k采样序列号，k=0,1,2,3...、Uk第k次采样时刻系统输出值、ek第k次采样时刻偏差值、ek-1第k-1次采样时刻偏差值、Ki=Kp*T/Ti、Kd=Kp*Td/T

发表于 2019-4-30 22:34

2、离散信号的PID控制器算法仿真：

1、位置式PID算法：

PID系统产生的值，完全作为系统的输入参数，即采用u(k)代替了r(k)，如果计算机出现故障时，位置式PID控制将导致Uk的剧烈变化，这会引起执行机构的大幅度变化，造成巨大损失。

仿真代码如下（python）：

复制

import matplotlib.pyplot as plt 

import numpy as np 

import random

import sys

import os



time_length = 600

time_sample = 100

time_interval = float(time_length/time_sample)

error_coeff = 3

t = np.linspace(0,time_length,time_sample)

Slope = 1

Intercept = 0

standard_in = 20



# The system model

system_model = lambda i : Slope*i + Intercept

standard_out = system_model(standard_in)

print("The Standard Output:%d" % standard_out)



Kp = 0.08 # average

Ki = -0.7 # intergre

Kd = 0.01 # diff



error_bef = []

real_out_ajust = []

real_out_ajust.append(70)

real_out_ajust.append(75)

error_bef.append(real_out_ajust[0]-standard_out)

Out_plt = np.linspace(standard_out,standard_out,time_sample)



# 标准直接计算公式1：Pout=Kp*e(t) + Ki*Sum[e(t)] + Kd*[e(t) - e(t-1)]

def PID_Controller_Direct_Mem(standard_out,t):

        global time_sample,Kp,Ki,Kd,error_bef,real_out_ajust

        if t > time_sample:

                print("Time Out! Quit!")

                return -1

        error_now = real_out_ajust[t] - standard_out

        error_bef.append(error_now) # 记录了所有的误差

        integrate_res = np.sum(error_bef)

        Diffirent_res = error_now - error_bef[t-1]

        return Kp*error_now + Ki*integrate_res + Kd*Diffirent_res



for t_slice in range(1,time_sample-1):

        Pout = PID_Controller_Direct_Mem(standard_out,t_slice)

        real_out_ajust.append(system_model(Pout))



plt.figure('PID_Controller_Direct_Mem')

plt.xlim(0,time_length)

plt.ylim(0,2*standard_out)

plt.plot(t,real_out_ajust)

plt.plot(t,Out_plt)

dhc053 · 发表于 2019-4-30 22:34

仿真结果如下所示：

图中所示，系统最终收敛于我们设定的红线的位置r(t)

发表于 2019-4-30 22:36

2、增量式PID算法：

当执行机构需要的控制量是增量而不是位置量的绝对数值是，可以采用增量式PID控制算法。

代码如下（python）：

复制

import matplotlib.pyplot as plt 

import numpy as np 

import random

import sys

import os



class PID_Prama:

        def __init__(self):

                self.Kp = 0

                self.Ki = 0

                self.Kd = 0

                self.set_val = 0

                self.error_last = 0

                self.error_prev = 0

                self.error_sum = 0



# 增量计算公式：

# Pout=Kp*[e(t) - e(t-1)] + Ki*e(t) + Kd*[e(t) - 2*e(t-1) +e(t-2)]

def PID_Controller_Increa(pid,out_now):

        error = pid.set_val - out_now

        Res = pid.Kp*(error-pid.error_last) + pid.Ki*error + \

              pid.Kd*(error-2*pid.error_last+pid.error_prev)

        pid.error_prev = pid.error_last

        pid.error_last = error

        return Res



PID_val = PID_Prama()

# PID参数

PID_val.Kp = 0.01

PID_val.Ki = 0.1

PID_val.Kd = 0.05

PID_val.set_val = standard_out # 标准输出值

# 增量型PID控制器输出值

PID_Controller_Increa_Out = []

Sys_In = []

# 0时刻系统输入值

Sys_In.append(5)

# 系统响应函数

SystemFunc = lambda x : 5*x + np.random.normal(0,0.5,1)[0]

Sys_Out = []

# 0时刻系统输出值

Sys_Out.append(SystemFunc(Sys_In[0]))

Time = 500

for t_slice in range(Time):

        Diff = PID_Controller_Increa(PID_val,Sys_Out[t_slice]) #系统误差

        PID_Controller_Increa_Out.append(Diff) # 记录所有的系统误差

        Sys_In.append(Sys_In[0]+np.sum(PID_Controller_Increa_Out)) # 计算增量之后的新的系统输入

        Sys_Out.append(SystemFunc(Sys_In[t_slice+1])) # 计算下一时刻系统新的输出值

standard = np.linspace(PID_val.set_val,PID_val.set_val,Time)

plt.figure('PID_Controller_Increa')

plt.xlim(0,Time)

plt.ylim(0,2*standard_out)

plt.plot(Sys_Out)

plt.plot(standard)

plt.show()

发表于 2019-4-30 22:36

这里对增量式PID算法进行深入的分析和计算：

No1：class PID_Param类保存了PID算法中的三个参数，Kp Ki Kd，同时类当中也记录了上一次系统存在的误差error_last，以及上上一次系统的误差error_prev，这样就能够完成增量式误差的公式计算。

No2：上述算法中在循环体中记录了所有的误差变量PID_Controller_Increa_Out，这是为了仿真的目的，实际上我们比不需要存储所有的误差参数。

No3：系统的响应system_model:

，系统后面添加了高斯噪声，这表示了系统在运行过程中的不稳定的过程，同时系统本身是一个线性系统，例如控制电机转速的系统：PWM--ctl--Speed

系统仿真结果：

[技术问答] PID控制算法的简单分析和仿真！

相关帖子

评论

浏览过的版块