|
例如在不具备浮点运算器的定点处理器使用定点运算,以前写过一篇Q格式的文章,有简单介绍过这些知识。 那么问题来了,有一个读者朋友的硬件平台无法使用,但是他要进行一些三角函数的运算,那么该如何自己动手实现呢? 下面我们来简单介绍一下整体的思路吧,因为硬件平台的资源比较紧张; RAM比较少; ROM比较少; CPU处理速度比较慢; 所以这里比较常用的方法就是通过空间换时间,预先将,的值存储到数组中,需要用的时候,访问数组就可以得到具体的数据。这也就是我们经常会提到的查表法。 下面我们来详细介绍一下。 正弦表 这个正弦函数表达式是这样的, 具体如下图所示;
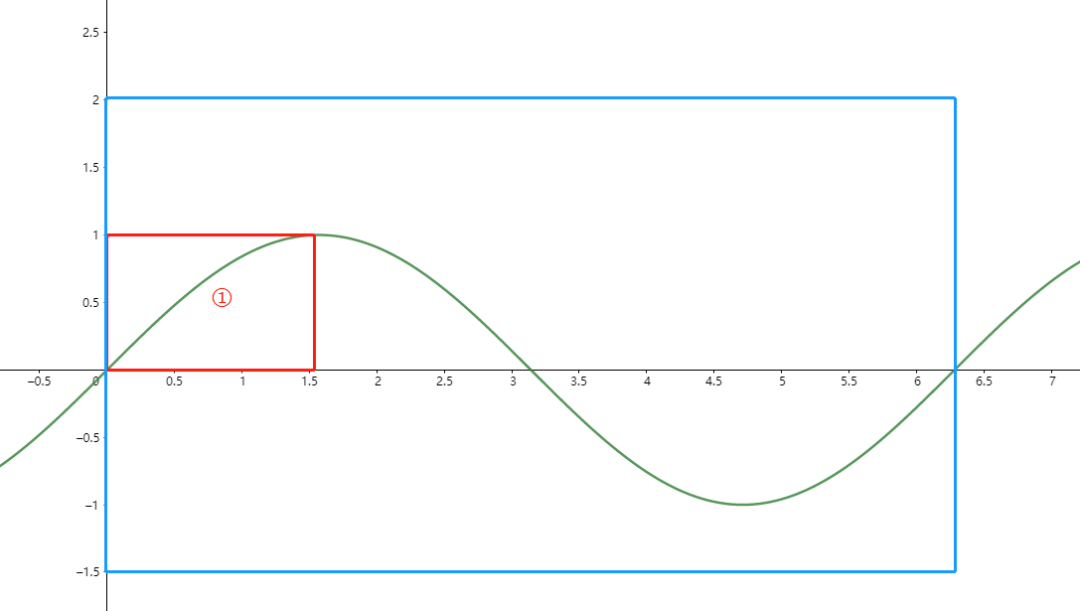
正弦波 首先我们来简单分析一下这个波形: 在蓝色框内是一整个周期的波形; 在红色框内是四分之一个周期的波形; 其实不难发现,我们只要表示出这四分之一个波形的数据,其余剩下的波形都可以通过换算表示出来。 这样做就大大节省了查表法所需要的空间。 下面我们来介绍一下具体如何实现; 首先我们得搞清楚一个点,就是量纲,统一用归一化的形式来做。 y的范围是 ; x的范围是,当然,x的范围也是没问题的,下面会继续介绍; 而在实际的程序中,我们是无法这样去做的,这些数值我们期望通过整形类型去访问,所以我们要做到几点: 尽量避免使用浮点运算; 尽量避免除法; 尽量避免乘法; 所以这里有必要先了解一下Q格式,用左移和右移去代替乘法和除法,提高运算效率; 对于X轴的数据,于是可以将细分成 128 ,256,512或者 1024 等等; 这里我们先细分成1024等份,正如前面提到的,只需要选择前四分之一周期的内容即可; 打印的输出结果如下:
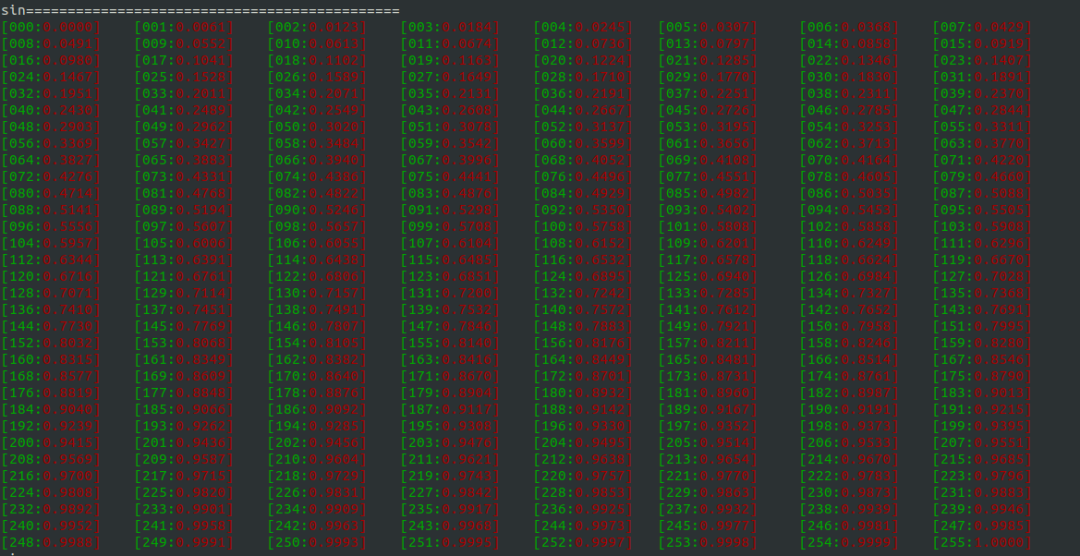
浮点类型的正弦表 这里我们可以简单取几个特殊点验证一下,发现整体还是可以接受的;
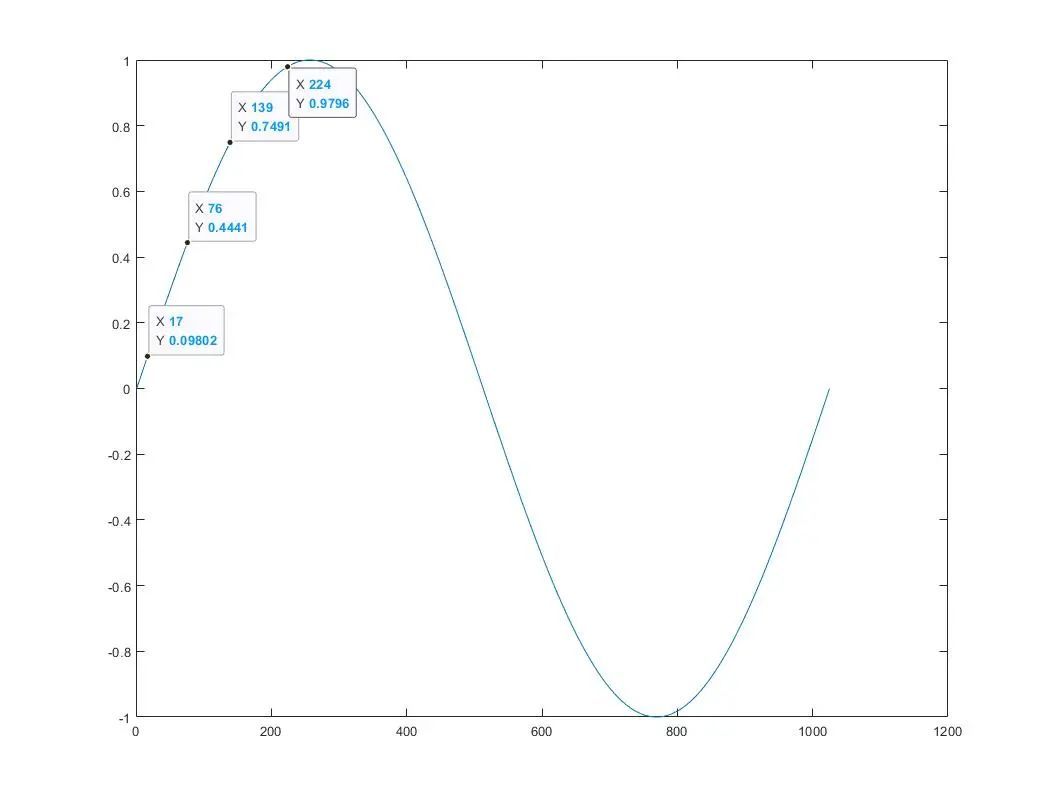
matlab输出的波形 下一步就是将浮点数据y转化为格式哈, 最终输出结果如下所示;
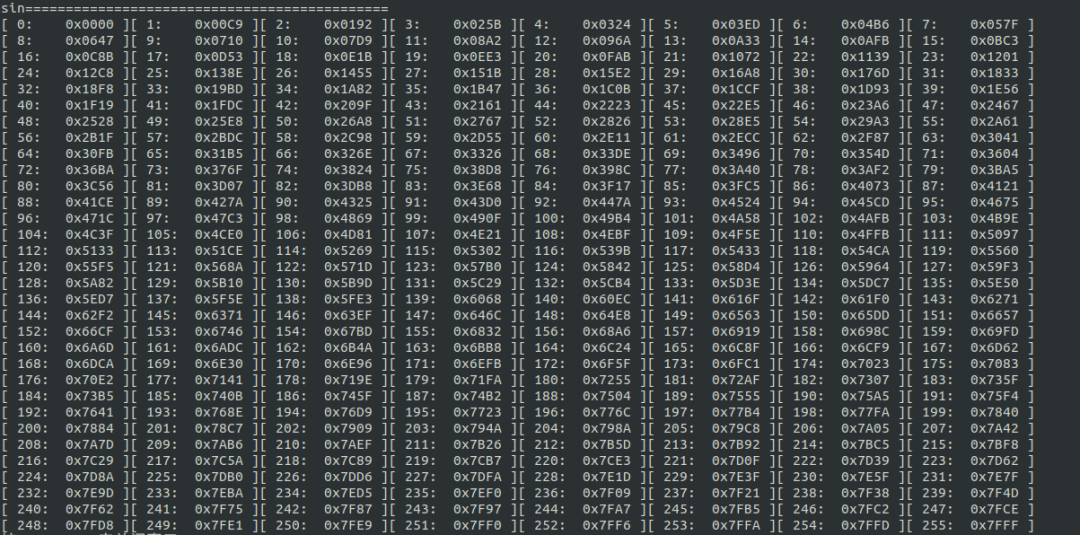
Q格式正弦表源码部分 下面这部分代码是参考的中的一个实例,下面我们会依次分析每个部分的作用,整体的代码具体如下所示; 由于输入的是格式,所以这里可以简单画个图;下面是角度从的示意图,如下所示;
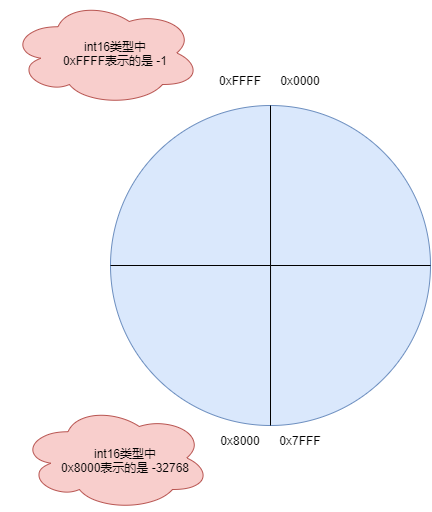
角度值 这里注意,负数是以补码形式进行保存的,正数的补码等于他本身; 负数的补码是除了符号位外,其他位取反,然后加上1; 所以可以算一下 表示; 表示 ; 因为Q格式中有无符号的范围和带符号的范围,所以这里的充分利用这个的数据,并且兼容了传入参数可以是有符号或者是无符号,这里比较绕,先看下面这张图片;
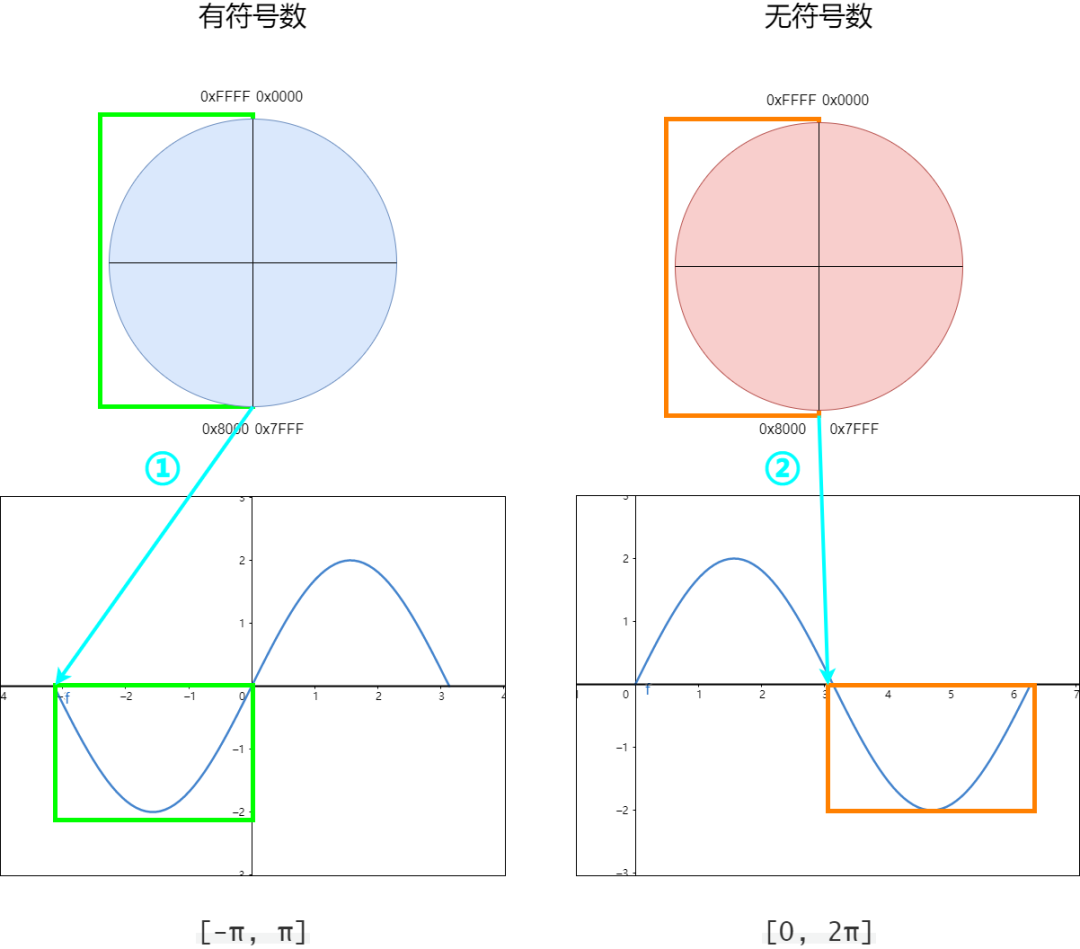
有符号和无符号 对比 上图中; 左边是有符号,右边是无符号数; 两个圆形分别表示和的数值范围; 左边绿色框内的波形相对应,橙色框内的波形相对应; 这里有几点我们要注意一下,无论是有符号和无符号,他们的周期都是相同的; 有符号整数 int16 :-32768 ~ 32765 , 无符号整数 uint16 :0 ~ 65535, 所以这两者都使用 65536个数来表示正弦的一个周期,也就是 2π。 这里是比较关键的地方,因此对于 0x8000 这个关键点,有符号和无符号所表示的数值是不同的; 有符号整数 int16 :0x8000 表示为 -32768; 无符号整数 uint16 :0x8000 表示为 32768; 因此这他们刚好相差了一个周期 65536,所以表示的正弦数值y是相同的,正如上图中蓝色箭头和所示。 内部实现 由于有符号整数 int16 的最高位是符号位,所以这里我们先把它转化成无符号整形; 前面用 类型是为了防止数据溢出,这里加上,相当于对正弦波平移了半个周期,所以在下面y和x的映射关系需要根据实际情况来修改; 因为前面提高过正弦表的四分之一是256个数据,所以整个正弦周期应该是 1024 个细分数据,那也就是2的10次,就需要 10 bit; 的数据范围是 ; 的数据范围是 ; 为了获取有效的高数据,对数据右移 ,具体如下所示;
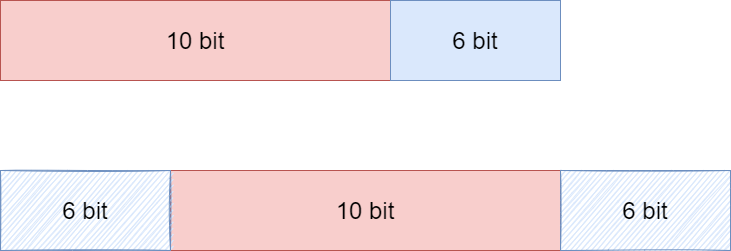
所以,我们又可以得到以下这个数据的范围 ,
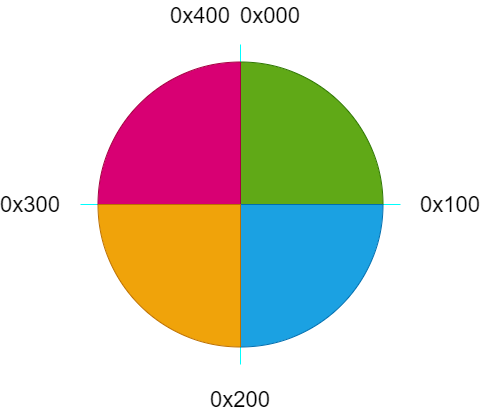
因此我们在程序中引入四个掩码,作为正弦波形落在哪个象限的标识位,这样也避免了使用除法运算,提高了效率,具体如下所示; 其中,表示 ,以此类推; 那为什么是这个映射关系呢? 0~90°不应该是从 吗?这里我们再简单解释一下; 前面有一个这样的操作,具体如下; 这里的加上,相当于加了一个,正弦波形向左移动了半个周期;因此整体的映射关系要和原始的数据对应起来,具体如下所示;
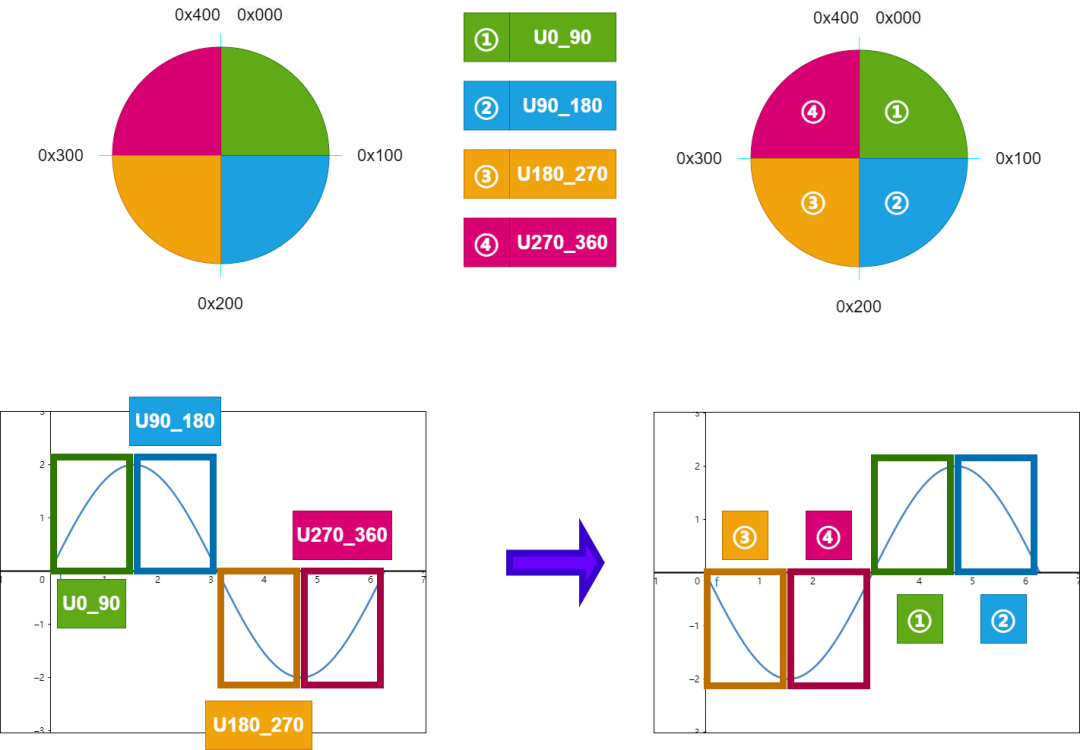
最后,既然我们已经知道波形在哪个象限了,就可以根据当前象限和我们正弦表的关系来得到新的波形,这里有中心对称,关于y轴对称,简单做一下变换就可以得到正弦值和余弦值;
|