几何学的分类---群论观点

1万 · 2024-3-4 16:25

《爱尔朗根纲领》在群论下统一当时的几何学各分支

1万 · 2024-3-4 16:26

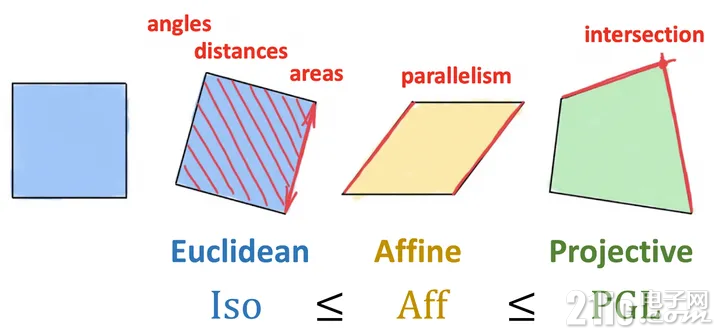
射影几何在群变换后研究的不变量包括了：线性（直线被变换后还是直线）、相交性（相交线被变换后还是相交线）、交比、保持圆锥曲线不变等等。而满足上述性质的变换群，即被称为“射影群”。

射影群的一个子群，被称为“仿射群”，对应于仿射几何的变换。仿射几何具有和欧氏几何相当类似的不变量，但是角度和长度是会改变的。

欧氏几何对应的变换群又是仿射群的一个子群，其不变量是旋转、平移和反射。

以下是一个示意图，表示了从射影几何—> 仿射几何 —> 欧氏几何的层层递进。其中列举的不变量，欧氏几何不变量：角度、距离和面积。仿射（affine）几何不变量：平行。射影几何的不变量：相交。

1万 · 2024-3-4 16:27

本帖最后由 keer_zu 于 2024-3-4 16:29 编辑

《爱尔朗根纲领》里所强调的变换群，在今天看来，是一种更广泛的群——李群的被称为“经典群”的特例。克莱因发表《纲领》十几年后，1884年，克莱因的好朋友、挪威数学家索菲斯·李在克莱因的基础上更详细讨论了变换群，他的三卷本的《变换群理论》引入了一般的连续变换群，今天的人称之为“李群”。
李群原本是数学家的游戏，威廉·基灵和嘉当继续发展了李群（还有李代数）。20世纪初，李群被大数学家外尔介绍进入了物理学，很快成为了物理学不可缺少的基本工具，我在后面很快就会谈到。

1万 · 2024-3-4 16:29

另外，《爱尔朗根纲领》里只考虑了均匀的空间，所以当时正在兴起的黎曼几何并没有被克莱因的变换群论囊括其中。但是不久之后，数学家们就把黎曼几何的“局部不变量”和克莱因的思想（变换群）结合起来。其中一个很有名的结果，叫做“嘉当联络”

几何学的分类---群论观点

相关下载

相关帖子

突出贡献奖章

沉静之湖泊

七世轮回

技术奇才奖章